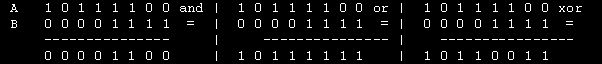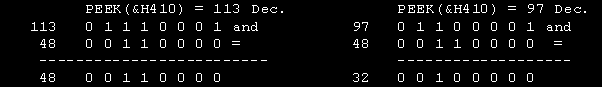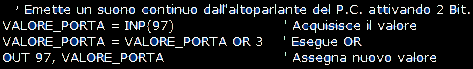Capitolo 6

GLI OPERATORI LOGICI e BOLEANI - I CODICI ASCII

Il microprocessore oltre ad alcune operazioni aritmetiche puo' svolgere anche le Operazioni Logiche.
Queste operazioni servono per effettuare confronti tra i dati ed attivare, in base ai risultati, una particolare azione.
Gli operatori logici vengono impiegati nelle Espressioni Boleane che costituiscono l'ossatura di tutti i programmi.
Le espressioni boleane fanno uso degli operatori relazionali e degli operatori logici e come risultato restituiscono un valore che viene inteso come vero o falso. Per fare un esempio se scriviamo :
IF A < B THEN PRINT"AAAA"
significa che se A e' minore di B l'espressione e' vera quindi verra' scritto AAAA .
Abbiamo usato l' operatore relazionale " < " ( minore ).
Al momento ci interesseremo degli operatori logici in quanto il loro impiego sui Bit e' determinante nelle operazioni di confronto.
I principali operatori logici sono: AND, OR, XOR, NOT
Altri due operatori, meno impiegati e presenti nel linguaggio Basic, sono IMP ed EQV.
Ogni operatore possiede la sua tabella della verita' che possiamo vedere eseguendo le operazioni logiche su una coppia di Bit.

Se consideriamo quanto sopra possiamo notare che l'operatore AND restituisce 1 quando A e B sono 1 mentre OR restituisce 1 se A o B oppure entrambi sono 1.
XOR restituisce 1 solo se o A o B sono 1 e NOT inverte 1 con 0 e viceversa.
IMP restituisce 0 solo se il secondo operatore e' 0 ed EQV restituisce 1 solo se ambedue gli operatori sono uguali.

Un esempio interessante sull'applicazione degli operatori logici e' dato dalla espressione che implica la decisione se appoggiare o meno un programma sostenuto da due dirigenti di una ipotetica ditta.
Il dirigente A approva il programma ( Si o NO ?)
Il dirigente B approva il programma ( Si o No ?)
L' espressione logica decidera' se approvare o meno il programma da parte mia.
Applicando NOT alla posizione di A = Si , io non approvero'. AND significa che se sia A che B approveranno anche io lo faro'.
OR fara' avere la mia approvazione se A oppure B approveranno. XOR mi fara' decidere di approvare se A oppure B, ma non entrambi, approveranno.
EQV e' il contrario di XOR quindi se sia A che B approveranno o sia A che B si opporranno, avranno il mio appoggio.
IMP significa che solamente se A approvera' e B si opporra' mi opporro' anch'io, mentre se sia A che B approveranno o sia A che B si opporranno o A si opporra' e B approvera', avranno il mio appoggio.

Torniamo ora ai nostri numeri ed alla loro relazione con gli operatori logici.
Una classica applicazione dell' operatore AND trova impiego nell'isolamento dei Bit o nell azzeramento di alcuni di essi mentre OR viene usato per attivare determinati Bit.
Esaminiamo alcune operazioni logiche:

Il risultato convertito in decimale ci dira' ben poco ma se prendiamo in esame il risultato in binario notiamo che l'operatore AND ha azzerato i 4 Bit superiori del valore A mentre OR ha portato ad 1 tutti i Bit inferiori ed infine XOR ha invertito i 4 Bit inferiori.
L'operatore logico NOT abbiamo detto che nega il valore preso in esame, cio' vuol dire che "lo complementa" ed infatti, considerando i valori A e B appena esaminati possiamo scrivere:

Abbiamo eseguito in questo modo la differenza con complemento a 2.
Nei linguaggi ad alto livello gli operatori logici vengono impiegati in cicli e strutture decisionali ed anche per isolare, azzerare o attivare certi Bit in operazioni che agiscono direttamente sulle locazioni di memoria.
Nei linguaggi a basso livello vengono impiegati per compiere operazioni sui Bit, Byte e Parole e prendere se il caso decisioni.
Vediamo qui di seguito alcuni esempi esplicativi:

Il Byte contenuto nella locazione 0410h contiene il tipo di adattatore video presente sul computer.
Il quinto Bit e' 0 se adattatore Colore Grafico o 1 se Monocromatico. Se l'adattatore e' Colore il risultato deve essere diverso da 30h o 48 Dec.
Vediamolo in binario:

L'espressione logica, in pratica, viene cosi' interpretata :
Se il valore alla locazione di memoria 0410h AND 30h e' diverso da 48 (30h), l'adattatore e' Colore-Grafico quindi intraprendi una certa azione.
Il valore 30h non e' arbitrario ma rappresenta la maschera che serve per isolare il Bit 4. ( Il quinto se consideriamo quello a destra come il primo Bit o il Bit 4 se consideriamo, come per definizione, il primo Bit come Bit 0 )
Come appena affermato la " Maschera " e' importantissima poiche' consente di operare sul Bit o sui Bit che opportunamente manipolati danno la possibilita' di conoscere lo stato di dispositivi collegati.
E' possibile, sempre impiegando una maschera appropriata, cambiare il valore contenuto nelle locazioni di memoria ed attivare o azzerare i Bit di stato delle " porte" attraverso cui il P.C. comunica con i dispositivi collegati.
Gli esempi che seguono ci dimostrano come ottenere lo stato della stampante e come manipolare l'altoparlante interno del P.C.

Per prima cosa viene acquisito l' indirizzo della porta relativo alla stampante LPT1 ( La stampante normalmente collegata )
Con l'istruzione INP preleviamo il Byte contenente il valore del registro di stato della stampante quindi eseguiamo un AND con il valore 8 che in questo caso rappresenta la maschera necessaria per isolare il Bit 3.
Se il valore e' 0, la stampante non e' abilitata se e' 1 essa e' abilitata.
Normalmente il valore prelevato differisce per motivi che non staremo ad approfondire ma il Bit 3 e' sempre 1 o 0.
Un valore classico di stampante abilitata e' costituito dalla seguente configurazione di Bit : 11011111
mentre la stampante non pronta o spenta puo' restituire 11110111 oppure 01110111 o altro dove il Bit 3 e' 0.
Se eseguiamo un AND con la maschera 8 ( 1000 binario ) vedremo che il Bit 3 sara' 1 nel caso di stampante abilitata e 0 negli altri casi.

Il valore acquisito contiene gli ultimi 2 Bit, il Bit 0 ed il Bit 1, a 0 Un valore tipico puo' essere 00110000.
Eseguendo un OR 3 ( 0011 in binario ) il valore cambia in 00110011 ed i Bit 0 e 1 vengono portati a 1 consentendo all'altoparlante di emettere un suono continuo.

Azzeramento di un registro       XOR AX,AX         Il valore in AX diventa 0
Azzeramento Byte Alto            AND AX,0FFh      Prima B4C2h dopo 00C2h
In questo ultimo esempio FFh rappresenta la maschera.

Nota: Ad alto livello l'operatore AND viene usato per unire due affermazioni logiche; a basso livello ispeziona i due operandi Bit per Bit e fornisce il risultato in base alla tabella della verita' esaminata all'inizio.
Cio' vale anche per gli altri operatori logici.

UN'ULTIMA CONSIDERAZIONE:
E' interessante notare la correlazione esistente tra una cifra binaria ed il relativo valore esadecimale.
Partendo dal valore 0 e spostando il valore 1 a sinistra di una posizione, la cifra binaria, come gia' affermato, corrisponde ad un valore decimale che aumenta esponenzialmente con potenza di 2.
Il valore Esadecimale , per contro, raddoppia e come risultato presenta una cifra che e'seguita da uno o piu' zeri. Vediamolo in pratica:


Quanto sopra e' stato messo in evidenza poiche' in alcuni casi la descrizione dei bit di stato di una periferica anziche' impiegare la dicitura :
Il Bit 7 vale 1
viene espressa come :
Il valore di ritorno e' uguale a 40h.
Dalla tabella possiamo notare che il valore 40h presenta il bit 7 uguale a 1.
Essendo, quanto visto fino ad ora, argomento molto importante, esso verra' ripreso man mano che se ne presentera' l'occasione.

I CODICI ASCII

I dati, lettere e numeri, per essere elaborati dal calcolatore devono essere codificati in forma binaria e viceversa, da questa forma devono essere decodificati per ricavare l'equivalente numero o lettera.
Per questo scopo e' stata creata una tabella di codici in grado di rappresentare tutte le lettere, i simboli ed i numeri.
Questi codici sono interpretati dal computer come una serie di numeri che va da 0 a 127 ( 0 - 01111111 ) ad ognuno dei quali corrisponde in maniera univoca un simbolo, una lettera o un numero.
Questi codici prendono il nome di CODICI ASCII ( American Standard Computer Information Interchange ) e rappresentano uno standard adottato da tutti i costruttori di calcolatori.

Il codice ASCII viene utilizzato nella trasmissione di dati verso le periferiche ( Video, Stampanti ) e nello scambio di dati tra calcolatori.
I codici si dividono in 3 categorie : Trasparenti, Simboli e numeri, Lettere.

I Codici Trasparenti hanno un valore che va da 0 a 31, non hanno corrispondenza nelle lettere dell'alfabeto e sono impiegati per trasmettere istruzioni di controllo.
I principali di questi sono il Codice 7 ( campanello ) ed a proposito se da Basic scriviamo : PRINT CHR$(7) udiremo un beep dall'altoparlante.
Il Codice 8 ( Back space ), il 12 ( Salto pagina ), il 13 ( A capo ), il 27 ( Escape ), ecc.

I Simboli e numeri vanno da 32 a 64 e comprendono vari simboli quali :
32 ( Spazio ), 43 ( + ), 45 ( - ), 46 ( . ), 61 ( = ), 64 ( @ ).
I numeri da 0 a 9 sono rappresentati dai codici che vanno da 48 ( 0 ) a 57 ( 9 ).
Le Lettere vanno da 65 ( A ) a 90 ( Z ) per le maiuscole e da 97 ( a ) a 122 ( z ) per le minuscole piu' altri simboli da 91 a 96 e da 123 a 127.
Notare che la differenza tra il numero che rappresenta il codice delle lettere minuscole e quello delle maiuscole e' 32, infatti 65 ( A ) + 32 = 97 ( a ).
Esiste poi una tabella estesa dei Codici ASCII i cui numeri associati vanno da 128 a 255. I caratteri rappresentati da 128 a 175 comprendono tutto quanto e' necessario per rispondere ai requisiti delle principali lingue europee.
I restanti rappresentano i simboli grafici per il tracciamento di riquadri e i caratteri matematici e scientifici.

E' importante non confondere l'immissione dati da tastiera con la codifica ASCII in quanto i tasti posseggono un loro codice di scansione che nulla ha in comune con la codifica in oggetto.
Il codice ASCII relativo al tasto pigiato, verra' reperito in memoria e dopo la decodifica visualizzato sullo schermo. La sequenza di queste operazioni verra' descritta in seguito.
Concludiamo ricordando che il numero associato al carattere determina la sequenza di ordinamento alfabetico dove i numeri vengono prima delle lettere maiuscole e queste prima delle minuscole.