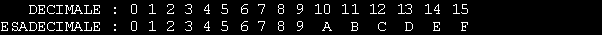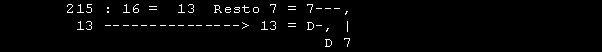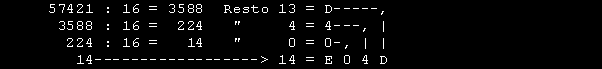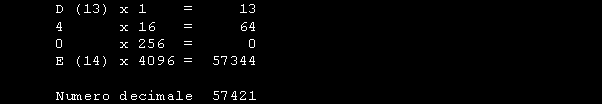|
Capitolo 3NOTAZIONE ESADECIMALE e OTTALENei calcolatori sono di uso corrente numeri binari composti da 8 cifre o multipli di 8 ( 16 o 32 ). Essendo pero' poco pratica l' indicazione di tali numeri in notazione binaria, si e' pensato bene di adottare un sistema di numerazione piu' compatto in:BASE 16 : La numerazione ESADECIMALE. Essa resta comunque un sistema di rappresentazione piu' comodo e semplice. Facendo un paragone tra il sistema Decimale e quello Esadecimale notiamo che le unita' decimali vanno da 0 a 9, le decine da 10 a 99, le centinaia da 100 a 999 e cosi' di seguito. In esadecimale le unita' vanno da 0 a 15, le "decine" da 16 a 255 le "centinaia" da 256 a 4095 ecc. Per definizione i numeri esadecimali vanno scritti seguiti da una h , questo per non confonderli con i decimali. Il numero decimale 20 e' diverso da 20h poiche' quest'ultimo vale 32 decimale. Anche la lettura e' diversa infatti 20h lo leggiamo due-zero mentre 20 lo leggiamo venti. Le cifre esadecimali da 0 a 15 sono rappresentate con i seguenti simboli:
Il gruppo di sinistra 1 0 1 0 lo chiameremo X Il gruppo di destra 0 0 0 1 lo chiameremo Y Considerando il gruppo di destra possiamo notare che se tutte le cifre fossero state 1 il massimo valore ottenuto sarebbe stato 15 decimale. Per ottenere 16 dobbiamo passare al gruppo di sinistra ( X ). Riassumendo : Il massimo valore ottenibile da un numero binario di 4 cifre e' 15. Per scrivere il valore superiore ( 15 ) dobbiamo passare sulla tabella di sinistra ( X ). Un gruppo di 4 cifre binarie rappresenta il sistema di numerazione in base 16. Il gruppo delle unita' esadecimali ( Y ) consente di rappresentare il valore massimo 15 decimale. Il gruppo a sinistra ( X ) inizia con il valore minimo 16 decimale ( 0 0 0 1 binario ) e rappresenta la base della numerazione ESADECIMALE IN BASE 16. Con riferimento al sistema posizionale per ogni spostamento a sinistra otterremo i valori: 1-16-256-4096-65536 ecc. quindi un incremento esponenziale in base 16. Adottando la notazione esadecimale ciascun gruppo di 4 cifre binarie consente di esporre un valore che va da 0 a 15. Esempio:
1 Conversione in binario 2 Conversione in esadecimale. Esaminiamo il numero decimale 215. Con il metodo gia' descritto otteniamo 1 1 0 1 0 1 1 1 binario
Valore tabella X = 13 Decimale --> D Esadecimale Valore Esadecimale totale = D7 Il secondo metodo di conversione impiega lo stesso sistema adottato per trasformare un numero decimale in binario con la differenza che si divide per 16. Esaminiamo ancora il numero 215 DECIMALE
Moltiplicando la parte intera x 16 si ottiene 3588 x 16 = 57408 Sottraendo questo valore a 57421 si ottiene 13 che e' il Resto. Medesima procedura per gli altri valori. Possiamo convertire facilmente il numero esadecimale in decimale. Sappiamo che il PESO DELLA POSIZIONE in notazione esadecimale vale , partendo da destra, 1-16-256-4096 ecc. Nel numero D7h alla cifra 7 corrisponde peso 1 quindi 7 x 1 = 7 Alla cifra D corrisponde peso 16 quindi D ( 13 decimale ) x 16 = 208 In conclusione 208 + 7 = 215. Applicando lo stesso principio a E 0 4 D otteniamo quanto segue:
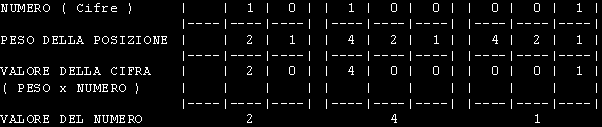
NOTAZIONE OTTALEEssa e' simile alla notazione Esadecimale ma i numeri vengono calcolati in base 8.I sistemi di conversione sono gli stessi gia' visti. Va aggiunto che i numeri ottali possono essere considerati come gruppi di 3 numeri binari infatti: Consideriamo ancora la cifra binaria 1 0 1 0 0 0 0 1 ( 161 decimale ).
La trasformazione da ottale in decimale avviene moltiplicando le cifre da destra a sinistra per la potenza crescente in base 8. ll numero 2 4 1 si sviluppa moltiplicando 1 x 1 = 1 4 x 8 = 32 2 x 64 = 128 quindi 128 + 32 + 1 = 161 decimale. Va ricordato a questo punto che la numerazione ottale e' poco impiegata e che normalmente, nei programmi, viene usata la notazione decimale ed esadecimale. La notazione binaria e' propria del calcolatore ma alcuni linguaggi permettono l'elaborazione di numeri in formato binario. Il programma DEBUG, facente parte dei programmi supplementari del MS-DOS o PC-DOS, assume che tutti i numeri digitati siano in formato esadecimale mentre il linguaggio Assembly assume che essi siano in formato decimale e quindi i numeri esadecimali devono avere il suffisso h ( 100h ). In Basic i numeri esadecimali vengono trattati come stringhe alfanumeriche con prefisso &H ( 15 = &HF) |