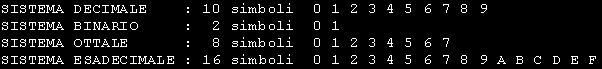Capitolo 1
ARITMETICA BINARIA ED ESADECIMALE
GLI OPERATORI BOLEANI
I CODICI ASCII
I Computer, essendo costruiti con componenti elettronici ed essendo di conseguenza dispositivi digitali riconoscono solamente DUE stati ON e OFF ossia
presenza o assenza di segnale. Su questo principio basilare si fonda la logica di funzionamento di tutti i calcolatori. La opportuna combinazione di questi
2 stati fa si che la macchina sia in grado di eseguire tutte le operazioni matematiche e logiche richieste dai programmi.
In conseguenza di quanto sopra, per eseguire le operazioni di calcolo, il computer non puo' adottare il nostro sistema decimale ma deve adottare un
sistema che gli sia congeniale IL SISTEMA BINARIO appunto.
Questo sistema si basa su due sole cifre 0 e 1.
Lo 0 rappresenta l' assenza di segnale e 1 la presenza quindi OFF e ON che sono i due stati che la macchina e' in grado di riconoscere.
LE BASI DELLA NUMERAZIONE
Il sistema piu' congeniale alla nostra logica e' il Sistema Posizionale; in esso ogni cifra ha il suo 'peso' cioe' un valore che dipende dalla sua posizione.
Il numero 5, ad esempio, e' inteso come 5 unita'; cambiando posizione verso sinistra ( 'shiftando' come si sentira' dire spesso in gergo informatico )
verra' inteso come 5 decine, cambiando ancora , come 5 centinaia, 5 migliaia e cosi' di seguito.
Si nota quindi che il numero cambia valore a seconda della posizione che assume ed ogni volta che viene spostato a sinistra viene moltiplicato per 10.
Il numero 10 e' la base del nostro sistema di numerazione che prende il nome di 'SISTEMA POSIZIONALE IN BASE 10' e 10 sono le cifre che lo compongono.
Partendo da questo concetto possiamo affermare che ad ogni spostamento verso sinistra corrisponde un valore dato dalla base ( 10 ) elevato alla potenza
della posizione assunta (4 posizioni = 10 ^ 3) .
Perche' 3 ? : Perche' la numerazione comincia da 0 e quindi 0 e' la prima posizione, 1 la seconda, 2 la terza ecc..
Note: Il simbolo ^ indica elevato a potenza.
Un esempio di numerazione con sistema non posizionale e' la numerazione
Romana dove 5 si scrive 'V' e per indicare 50 non ci si sposta di una
posizione a sinistra ma si scrive 'L'.
L' esempio che segue mostra come viene interpretato un numero in base 10 e
piu' precisamente il numero 1024
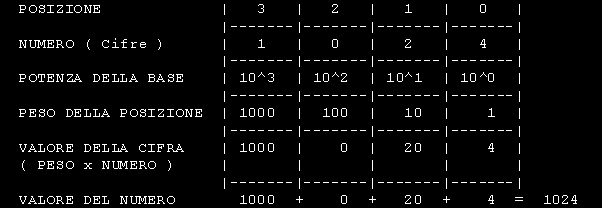
Il PESO DELLA POSIZIONE
e' uguale al Valore della base ( nel nostro caso 10 ) elevato al valore della POSIZIONE.
Ogni cifra viene ricavata moltiplicando il PESO DELLA POSIZIONE per il NUMERO contenuto nella
relativa colonna.
In pratica il numero che vogliamo identificare , 1024 lo ricaviamo in questo modo:
1a posizione:
vale 0 quindi 10^0 dara' come risultato 1 che moltiplicato per il numero contenuto nella relativa
colonna sara' uguale a 4 ( 1 x 4 = 4 )
2a posizione:
vale 1 quindi 10^1 dara' come risultato 10 che moltiplicato per il numero contenuto nella relativa
colonna sara' uguale a 20 ( 10 x 2 = 20 )
3a posizione:
vale 2 quindi 10^2 dara' come risultato 100 che moltiplicato per il numero contenuto nella relativa
colonna sara' uguale a 0 ( 100 x 0 = 0 )
4a posizione:
vale 3 quindi 10^3 dara' come risultato 1000 che moltiplicato per il numero contenuto nella relativa
colonna sara' uguale a 1000 ( 1000 x 1 = 1000 )
Il valore finale e' ottenuto sommando le cifre ricavate.
Il principio sopra esposto e' ugualmente valido con il SISTEMA BINARIO in quanto anch'esso e' un sistema posizionale ma con una sostanziale differenza:
La sua base NON e' piu' 10 ma 2, quindi esso e' un: SISTEMA POSIZIONALE IN BASE 2
Anche se i computer riconoscono ed interpretano diversi sistemi di numerazione, quello che sta' alla base del loro funzionamento e' quello BINARIO che
rispecchia i 2 stati riconosciuti dalla macchina : ON-OFF.
Oltre al sistema BINARIO vengono impiegati il sistema DECIMALE, OTTALE ed ESADECIMALE. Questi ultimi sistemi sono solamente rappresentativi e sono
impiegati per evitare di dover digitare e quindi visualizzare enormi sequenze di 1 e 0 .
Ricapitolando :
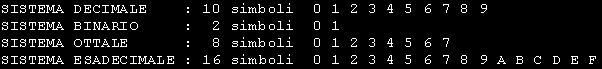
|