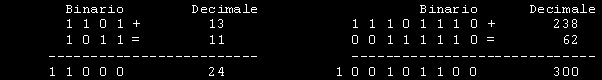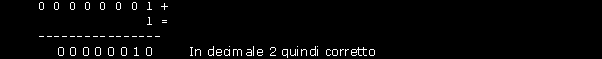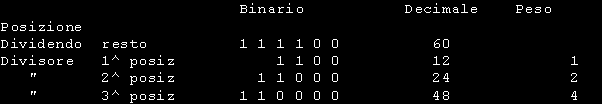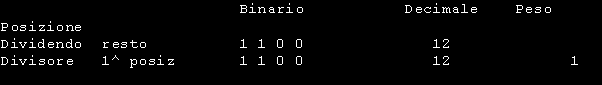|
Capitolo 4OPERAZIONI IN NOTAZIONE BINARIAMolto spesso e' necessario eseguire a mano i calcoli in binario specialmente in relazione all'ottenimento di risultati in operazioni logiche.Occorre tener presente che i valori numerici possono essere rappresentati come valori assoluti o valori con segno. Considerando un Byte, con gli 8 bit che lo compongono possiamo esprimere un valore assoluto pari a: Possiamo quindi affermare che con 1 Byte andremo a visualizzare 256 simboli numerici da 0 a 255. Sempre considerando gli 8 bit il valore con segno va da -128 a +127 poiche’ il bit piu’ significativo, quello di sinistra, e’ riservato per identificare il valore positivo o negativo. Nei numeri con segno vengono considerati i primi 7 bit partendo da destra e quindi se l’ottavo e’ 0 il numero’ sara’ positivo 01111111 (127) mentre se sara’ uguale a 1 il numero si considerera’ negativo 10000000 (-128) Gli esempi seguenti si riferiranno ad operazioni con numeri assoluti quindi senza segno. SOMMA BINARIALa somma binaria si esegue tenendo presente che quando il risultato e' 2 si scrive 0 e si esegue il riporto di 1.Esempi:
MOLTIPLICAZIONE BINARIALa moltiplicazione binaria si esegue con lo stesso criterio della moltiplicazione decimale con la differenza che essendo in base 2 il valore del moltiplicando rimane uguale se la cifra del moltiplicatore e' 1 e diventa 0 se il moltiplicatore e' 0.Per ogni cifra del moltiplicatore viene eseguito uno spostamento a sinistra e quindi si addizionano le colonne ottenute. Vediamolo con un esempio:
SOTTRAZIONE BINARIA E COMPLEMENTO A 2Per motivi inerenti alla logica del computer la sottrazione viene eseguita con il metodo del complemento.Il complemento di un numero binario richiede semplicemente l'inversione delle sue cifre ossia tutti gli 0 diventano 1 e tutti gli 1 diventano 0. La sottrazione comporta quindi il complemento del sottraendo e successivamente la somma dei due numeri. Questa operazione eseguita in complemento a 1 non e' pero' corretta in quanto comporta dei risultati sbagliati. Per evitare errori si accede ad una seconda fase, da qui il complemento a 2, che richiede la somma di 1 al risultato e l'eliminazione del primo BIT di sinistra. Vediamo ora alcuni esempi in cui i numeri binari saranno rappresentati con 8 Bit. Proviamo ad eseguire 6 - 4 = 2
Se aggiungiamo 1 al risultato otterremo:
Altro esempio: 225 - 187 = 38
Riassumendo : La sottrazione binaria si esegue sommando la prima cifra alla seconda complementata, aggiungendo 1 al risultato ed eliminando la prima
cifra a sinistra del risultato finale. DIVISIONE BINARIAGli esempi seguenti sono solo dimostrativi in quanto questo tipo di operazione non verra' mai eseguita manualmente.Eseguiamo questa divisione : 32 : 15 = 2 con resto 2
Altro esempio :
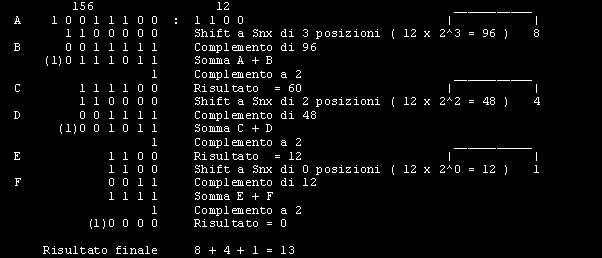
Il divisore 1 1 0 0 viene spostato a sinistra fino ad ottenere un valore il piu' vicino possibile a quello del dividendo ( 1 0 0 1 1 1 0 0 ) ma inferiore allo stesso. Poiche' ad ogni spostamento il divisore viene raddoppiato, otterremo quanto segue:
La quarta posizione ha come peso 8 quindi il primo valore ottenuto e' 8 ed e' la prima cifra che verra' sommata alle altre ricavate nei passaggi successivi e che alla fine ci forniranno il risultato finale. Il valore 96 viene sottratto da 156 con il metodo del complementato a 2 e come risultato otteniamo 1 1 1 1 0 0 ( 60 dec.) Ripetiamo la procedura precedente :
Quanto abbiamo appena visto risulta parecchio complicato e per nulla pratico, e' consigliabile eseguire le nostre operazioni in notazione decimale e poi convertire il risultato in binario. |