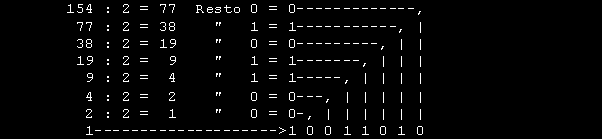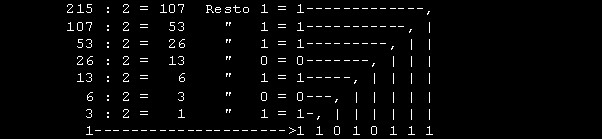|
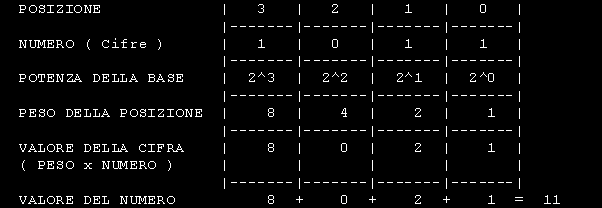
Capitolo 2NOTAZIONE BINARIAPrima di procedere con il lavoro sui numeri binari chiariamo un concetto che sta alla base della nomenclatura informatica.Sentiremo spesso parlare di BIT, NIBBLE, BYTE, WORD, DOUBLE WORD Il BIT ( forma contratta della parola BINARY DIGIT ossia CIFRA BINARIA ) e' la piu' piccola quantita' di informazione concepibile e puo' indicare la scelta tra DUE soli stati; puo' rappresentare uno stato fisico di un dispositivo ( Acceso o Spento ON-OFF ) ma puo' anche rappresentare uno stato logico ( Vero o Falso , Si o No) ed ancora, una alternativa tra due possibilita'. I numeri, per essere elaborati, devono essere quindi convertiti in forma binaria all'interno del computer. Per motivi di efficienza i computer lavorano contemporaneamente su gruppi di BIT, di solito 8 o multipli di 8, e si dice quindi che lavorano a 8 o 16 o 32 BIT. Un insieme di 8 BIT prende il nome di BYTE 16 BIT o 2 BYTE prendono il nome di WORD o PAROLA 32 BIT o 4 BYTE prendono il nome di DOUBLE WORD o DOPPIA PAROLA. Il NIBBLE e' formato da 4 BIT. Le cifre binarie sono rappresentate da singoli BIT, ogni cifra e' 1 BIT che puo' valere 0 o 1. La notazione binaria permette di indicare qualsiasi quantita' facendo uso di soli 2 simboli ed il procedimento di interpretazione posizionale e' analogo a quello in base 10 con la differenza che le cifre, in base alla posizione occupata verranno moltiplicate per potenze in base 2. L' esempio che segue mostra come viene interpretato un numero in base 2 e piu' precisamente il numero 1011 ( 11 DECIMALE )
Ogni cifra viene ricavata moltiplicando il PESO DELLA POSIZIONE per il NUMERO contenuto nella relativa colonna. Il valore finale e' ottenuto sommando le cifre ricavate. Come si puo' notare questo ultimo numero e' formato da 8 BIT ( 1 BYTE ) ed essendo tutti i BIT a 1 , rappresenta il massimo valore attribuibile ad 1 BYTE . L' uso di un raggruppamento di 8 simboli e' un dato basilare nei computer. Vista la scomodita', a causa dell'elevato numero di cifre, di impiegare direttamente il sistema binario da parte nostra, e' stato introdotto il sistema OTTALE ed ESADECIMALE. Questi sistemi permettono di adoperare una simbologia adatta al modo di funzionare da parte del calcolatore. L'impiego dei vari sistemi di numerazione non cambia il valore di un numero ma solo la sua simbologia. Il calcolatore utilizza comunque sempre e solo il sistema BINARIO. Visto il modo di convertire un numero BINARIO in DECIMALE verra' portato un esempio di conversione da DECIMALE a BINARIO. Esaminiamo il numero 154 DECIMALE
Il procedimento e' molto semplice, si divide per 2 il numero DECIMALE e partendo da DESTRA verso SINISTRA si scrive 0 se non c'e' resto e 1 se c'e' resto. Il risultato della divisione viene ancora diviso per 2 fino ad ottenere 1. Esaminiamo ancora il numero 215 DECIMALE
Si puo' controllare convertendo il numero binario in numero decimale.
In Binario lo si moltiplica per 2 , in Ottale per 8, in decimale per 10 ed in esadecimale per 16. E' questa una regola che trova un massiccio impiego nel calcolo dei segmenti di memoria o di indirizzi in notazione Esadecimale. Non dimenticarlo. |