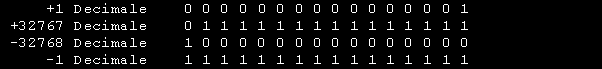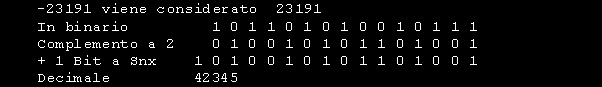Capitolo 5

OPERAZIONI IN NOTAZIONE OTTALE, ESADECIMALE, I NUMERI NEGATIVI

Le operazioni esaminate fino ad ora possono essere eseguite sia in OTTALE che in ESADECIMALE. Le procedure sono del tutto simili a quelle usate in notazione Decimale, bisogna solo tenere presente che in Ottale il valore piu' alto di una singola cifra e' 7 mentre in Esadecimale e' 15. Dopo questi valori si esegue il riporto. Esaminiamo qui di seguito alcuni esempi.

ADDIZIONE

In ottale sommando 5 + 5 si ottiene 12 quindi scrivo 2 e riporto di 1 al 4
In esadecimale 5 + 5 = A mentre E + 4 = 12

SOTTRAZIONE

La sottrazione avviene in modo diretto come in decimale tenendo presente che la cifra presa in prestito dalla colonna a sinistra, quando necessario, e che rappresenta 10 in decimale, varra' 10h ( 16 dec ) in Esadecimale e 10 Oct.( 8 dec) in Ottale.
Esempio :

Come si puo' notare nell' esempio in esadecimale il primo passaggio prevede la sottrazione 3 – 9.
Prendiamo in prestito da Eh (la cifra E che compone il numero E3) 10h e lo convertiamo nel corrispondente valore decimale 16.
Lo sommiamo a 3 ed otteniamo 19.
Sottraiamo 9 da 19 ed otteniamo 10 dec. Che corrisponde a Ah.
Eh a causa del riporto, scala di 1 e diventa Dh ( 13 dec ) da cui togliamo 7 ed otteniamo 6. Il risultato finale 6Ah

La Moltiplicazione e la Divisione in Ottale ed Esadecimale seguono, come gia' detto, le regole delle analoghe operazioni decimali tenendo presente il differente valore attribuito al simbolo 10. Riporteremo un breve esempio di moltiplicazione e divisione in Esadecimale.

Per controllare i risultati basta convertire in decimale ed eseguire i calcoli.
Chiudiamo questo paragrafo ricordando che la maggior parte delle moltiplicazioni e divisioni in binario o in esadecimale verranno eseguite in potenze di 2 o di 16 e tali operazioni, come gia' visto si eseguono aggiungendo o togliendo uno 0 dalla cifra in oggetto.
Una applicazione abbastanza frequente e' il calcolo dell' indirizzo assoluto di un segmento di memoria.
Senza entrare nel merito dell'argomento relativo alla memoria del computer,si sappia che un indirizzo assoluto si calcola moltiplicando il valore del segmento x 16 ed aggiungendo lo spiazzamento ( Offset di segmento).
Ad esempio l' indirizzo assoluto della locazione A216:C321 si ottiene moltiplicando A216h x 10h = A2160h e sommando C321h ottenendo quindi AE481h .

I NUMERI NEGATIVI

Fino ad ora abbiamo sempre fatto riferimento a numeri interi positivi senza segno.
Per la sua architettura interna a 16 Bit il microprocessore puo' gestire numeri interi formati da 1 Byte o da 1 Parola ( 2 Byte ).
I valori vanno da 0 a 255 (FFh) e da 0 a 65535 (FFFFh)
Se impieghiamo solo 7 o 15 Bit possiamo gestire numeri che vanno da : 0 a 127 (7Fh) e da 0 a 32767 (7FFFh).
Poiche' i microprocessori di nostro interesse sono a 16 Bit prenderemo in esame il valore dei numeri con segno che va da -32768 a +32767. Vediamo alcuni di questi numeri in formato binario :

Come possiamo notare i due gruppi di uguale lunghezza si differiscono per il primo Bit a sinistra che e' 0 o 1.
Se il primo Bit a sinistra lo interpretiamo come Bit di segno, 0 se numero positivo ed 1 se numero negativo, avremo da +1 a +32767 con il primo Bit a 0 e da -1 a -32768 con il primo Bit a 1.
Il Bit a sinistra e considerato come il Bit piu' significativo e per brevita' lo indicheremo con la sigla informatica MSB (Most Significant Bit)
Per capire perche' 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 viene interpretato come -1 dobbiamo per un attimo rifarci alla notazione in complemento a 2.
Quando il numero esaminato ha il MSB a 1 vengono presi in esame i 15 Bit a destra , essi vengono complementati ed al risultato viene aggiunto 1. Il numero ottenuto e' considerato con segno - quindi negativo. Esaminiamo alcuni numeri:

Da questo esempio si comprende che un numero negativo e' il complemento di un numero positivo senza segno compreso tra 32767 e 65535 e di conseguenza lo stesso numero positivo senza segno viene ricavato complementando il negativo ed aggiungendo 1 a sinistra.
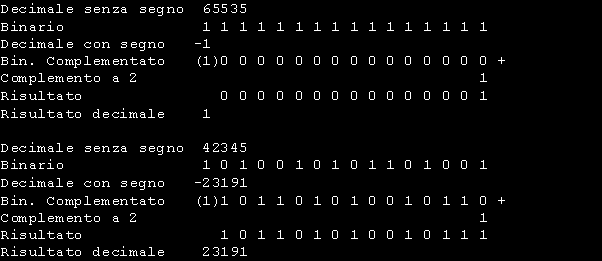
Per meglio comprendere:

Esiste un metodo molto piu' semplice che e' quello di sommare 65536 al numero negativo , infatti -23191 + 65536 = 42345
Un' ultima considerazione:
In alcuni linguaggi ( Assembly, Pascal, C ) e' facolta' del programmatore definire un numero con segno o senza segno quindi il massimo valore ottenibile puo' andare da 0 a 65536 o da -32768 a +32767.
In BASIC ( Linguaggio ad alto livello ) i numeri interi sono solo con segno.
Se eseguiamo questa linea di programma:
PRINT &HC456 il computer restituira' -15274.
La spiegazione e’ semplice:
C456h corrisponde a 50262.
Poiche’ il range dei numeri interi in Basic va da -32.768 a +32.767 i valori positivi oltre quest’ultimo valore sono interpretati come negativi e quindi 50262 viene complementato ed il risultato e’ appunto 15274 con segno -.
Concluderemo la panoramica sulle rappresentazioni numeriche esaminando come il computer elabora i numeri superiori ai valori fino ad ora considerati.
Come abbiamo appena visto i numeri interi possono venire espressi con un massimo di 2 Byte in quanto le capacita' intrinseche del microprocessore a 16 Bit consentono di operare aritmeticamente solo su questo formato.
Va segnalato che il microprocessore a 32 Bit estende il formato in esame.
Con appropriati programmi possiamo aumentare le capacita' operative della macchina consentendole di elaborare numeri molto piu' grandi.
I linguaggi di programmazione, come ad esempio il Basic, permettono di elaborare numeri in 4 formati diversi e precisamente:

Come possiamo notare i numeri in semplice e doppia precisione possono rappresentare valori enormi.
Questi numeri sono anche detti in virgola mobile e vengono rappresentati in notazione scentifica che consta di due parti, la prima rappresenta le cifre che compongono il numero e la seconda la posizione della virgola decimale; dal momento che la virgola puo' essere spostata liberamente essi possono diventare molto estesi o frazioni piccolissime.
Indipendentemente dal linguaggio di programmazione usato i numeri occupano una dimensione ben precisa in memoria.
Gli Interi occupano 2 Byte, gli Interi Lunghi 4 Byte , quelli in Semplice Precisione 4 Byte e quelli in Doppia Precisione 8 Byte.
I numeri Interi vengono codificati nel loro reale formato mentre per i numeri in virgola mobile i Byte interessati non contengono le cifre effettive del numero ma dei riferimenti che opportunamente decodificati restituiscono il valore memorizzato.